发表更新Java19 分钟读完 (大约2831个字)

Java中的NIO学习笔记

流与块的比较原来的 I/O 库(在 java.io.*中) 与 NIO 最重要的区别是数据打包和传输的方式。正如前面提到的，原来的 I/O 以流的方式处理数据，而 NIO 以块的方式处理数据。面向流 的 I/O 系统一次一个字节地处理数据。一个输入流产生一个字节的数据，一个输出流消费一个字节的数据。
阅读更多
发表更新Java4 分钟读完 (大约527个字)

try、catch、finally与return的执行顺序问题

finally一定会执行return以最后一次为准return后的finally是否修改了数据，得看具体类型try{} catch(){}finally{} return按照正常的顺序执行：有错会执行catch，finally都会执行，最后执行return。 private static in
阅读更多
发表更新数据结构与算法5 分钟读完 (大约822个字)

HDOJ 1003 最大子序列和

这道关于DP的经典题终于花时间弄明白了。一定要记录一下啊。题目链接。思路对这个题目，其实最重要的是思路。参考了此博客上面的思路，在这里对DP求解的思路做一些整理。设数组$arr$的长度为$n$，下标从$0$到$n-1$，则最后一个元素表示为$arr[n-1]$。对连续和最大的子数组（后称"
阅读更多
发表更新Android13 分钟读完 (大约1988个字)

从Android源代码来看WiFi直连

什么是WiFi直连通俗点说，它可以不通过网络，也不通过蓝牙，只要两台设备都支持WiFi直连，打开WiFi，不用连接任何WiFi，就可以进行信息的传输（请忽略下面两张图中的WiFi连接标志，因为其与WiFi的连接与否无关，打开就可以）。在Android的设置->网络与互联网->WLAN-&
阅读更多
发表更新Java31 分钟读完 (大约4596个字)

Java中的值传递

在知乎上面看到的关于Java中值传递与引用传递的回答，非常赞！回答一作者：Intopass链接：https://www.zhihu.com/question/31203609/answer/50992895来源：知乎著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。首先，不要纠结于
阅读更多
发表更新中间件11 分钟读完 (大约1632个字)

基于Netty实现局域网内自动组网

这种功能的实现首先考虑到的是广/多播，然后通过所受到的广播，获取到发送某种广播的ip地址，即实现“发现设备”功能。得到IP，即完成组网功能。多播与广播在这里选择的是多播。选项|单播|多播（组播）|广播:|:|:|:描述|主机之间一对一的通讯模式，网络中的交换机和路由器对数据只进行转发不进行复制。|主
阅读更多
发表更新数据结构与算法12 分钟读完 (大约1873个字)

二叉树的(迭代式)遍历

终于到写这篇的时候了。这是一篇对于邓俊辉的《数据结构(C++语言版)(第3版)》中二叉树遍历部分的读书笔记，图片来自DSACPP。感觉这本书很用心。当初要买这本书的原因也就是看到了他对迭代式遍历二叉树的这些内容，很赞。

先序遍历

图05-32.先序遍历过程：先沿左侧通路自顶而下访问沿途节点，再自底而上依次遍历这些节点的右子树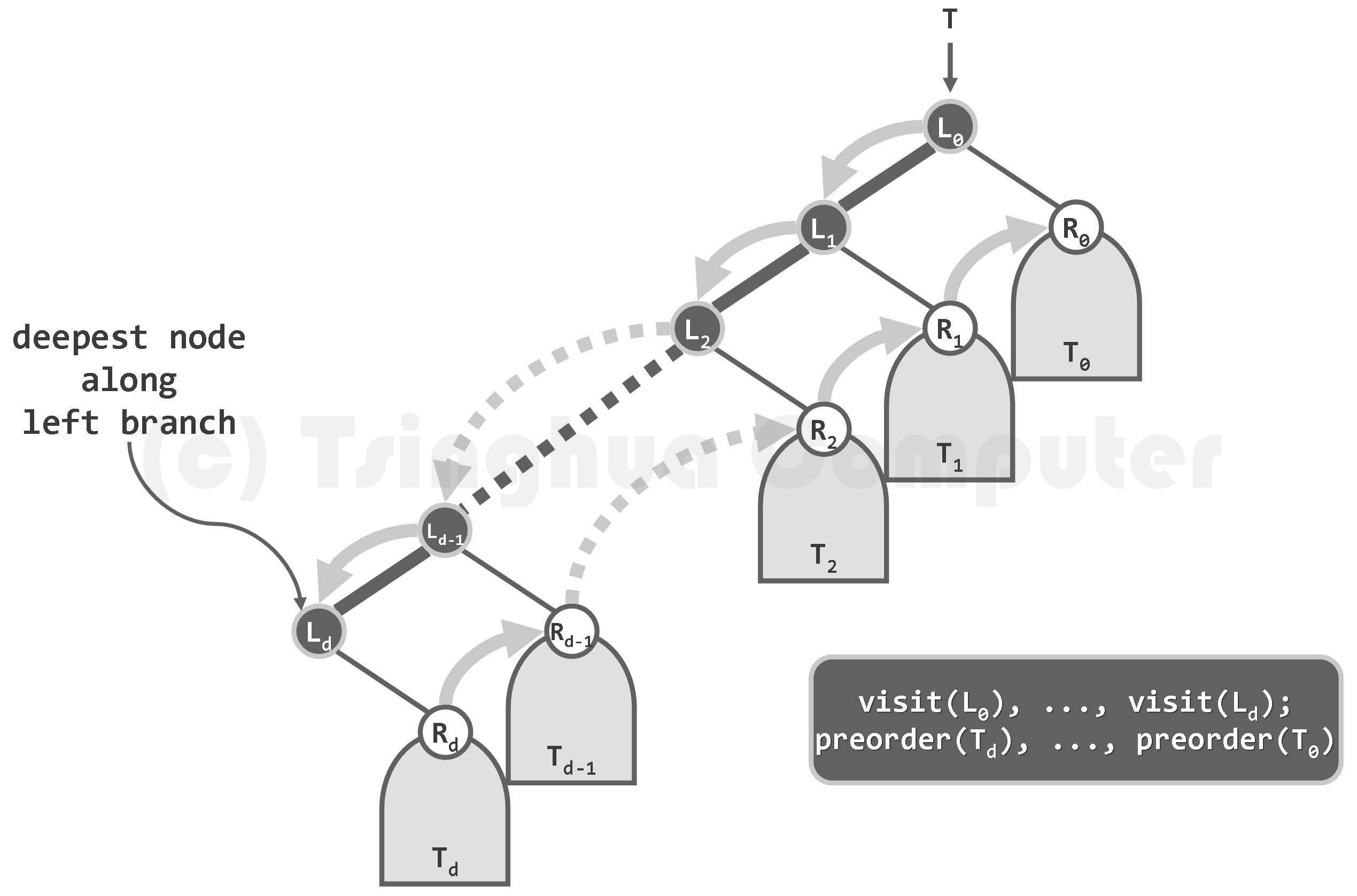
这里写图片描述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/******************************************************************************************
 * Data Structures in C++
 * ISBN: 7-302-33064-6 & 7-302-33065-3 & 7-302-29652-2 & 7-302-26883-3
 * Junhui DENG, [email protected]
 * Computer Science & Technology, Tsinghua University
 * Copyright (c) 2006-2013. All rights reserved.
 ******************************************************************************************/

#pragma once

//从当前节点出发，沿左分支不断深入，直至没有左分支的节点；沿途节点遇到后立即访问
template <typename T, typename VST> //元素类型、操作器
static void visitAlongLeftBranch ( BinNodePosi(T) x, VST& visit, Stack<BinNodePosi(T)>& S ) {
   while ( x ) {
      visit ( x->data ); //访问当前节点
      S.push ( x->rc ); //右孩子入栈暂存（可优化：通过判断，避免空的右孩子入栈）
      x = x->lc;  //沿左分支深入一层
   }
}

template <typename T, typename VST> //元素类型、操作器
void travPre_I2 ( BinNodePosi(T) x, VST& visit ) { //二叉树先序遍历算法（迭代版#2）
   Stack<BinNodePosi(T)> S; //辅助栈
   while ( true ) {
      visitAlongLeftBranch ( x, visit, S ); //从当前节点出发，逐批访问
      if ( S.empty() ) break; //直到栈空
      x = S.pop(); //弹出下一批的起点
   }
}
//***************************************************************
template <typename T, typename VST> //元素类型、操作器
void travPre_I1 ( BinNodePosi(T) x, VST& visit ) { //二叉树先序遍历算法（迭代版#1）
   Stack<BinNodePosi(T)> S; //辅助栈
   if ( x ) S.push ( x ); //根节点入栈
   while ( !S.empty() ) { //在栈变空之前反复循环
      x = S.pop(); visit ( x->data ); //弹出并访问当前节点，其非空孩子的入栈次序为先右后左
      if ( HasRChild ( *x ) ) S.push ( x->rc ); if ( HasLChild ( *x ) ) S.push ( x->lc );
   }
}

图05-31.迭代式先序遍历实例（出栈节点以深色示意）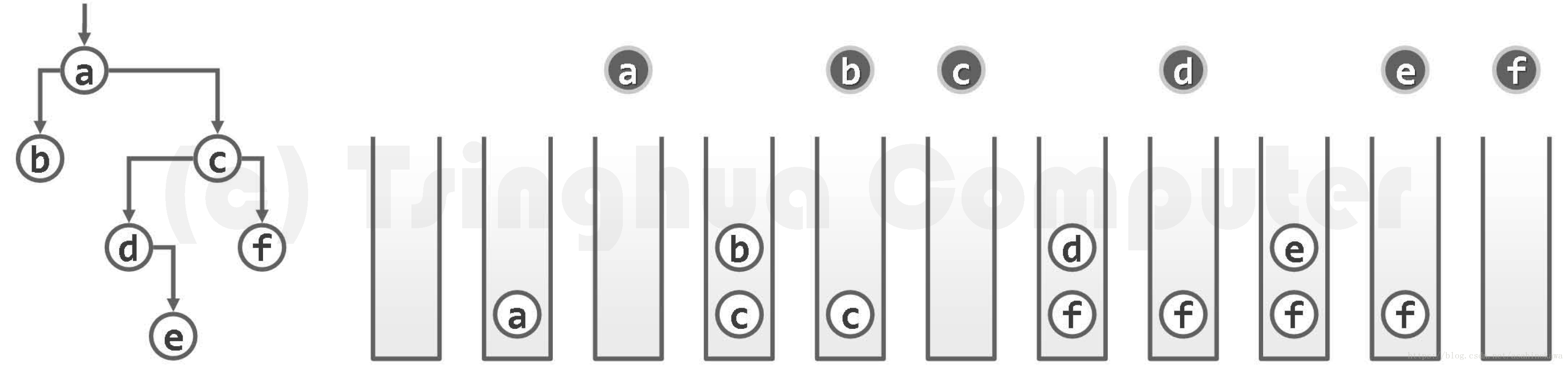
这里写图片描述

中序遍历

图05-33.中序遍历过程：顺着左侧通路，自底而上依次访问沿途各节点及其右子树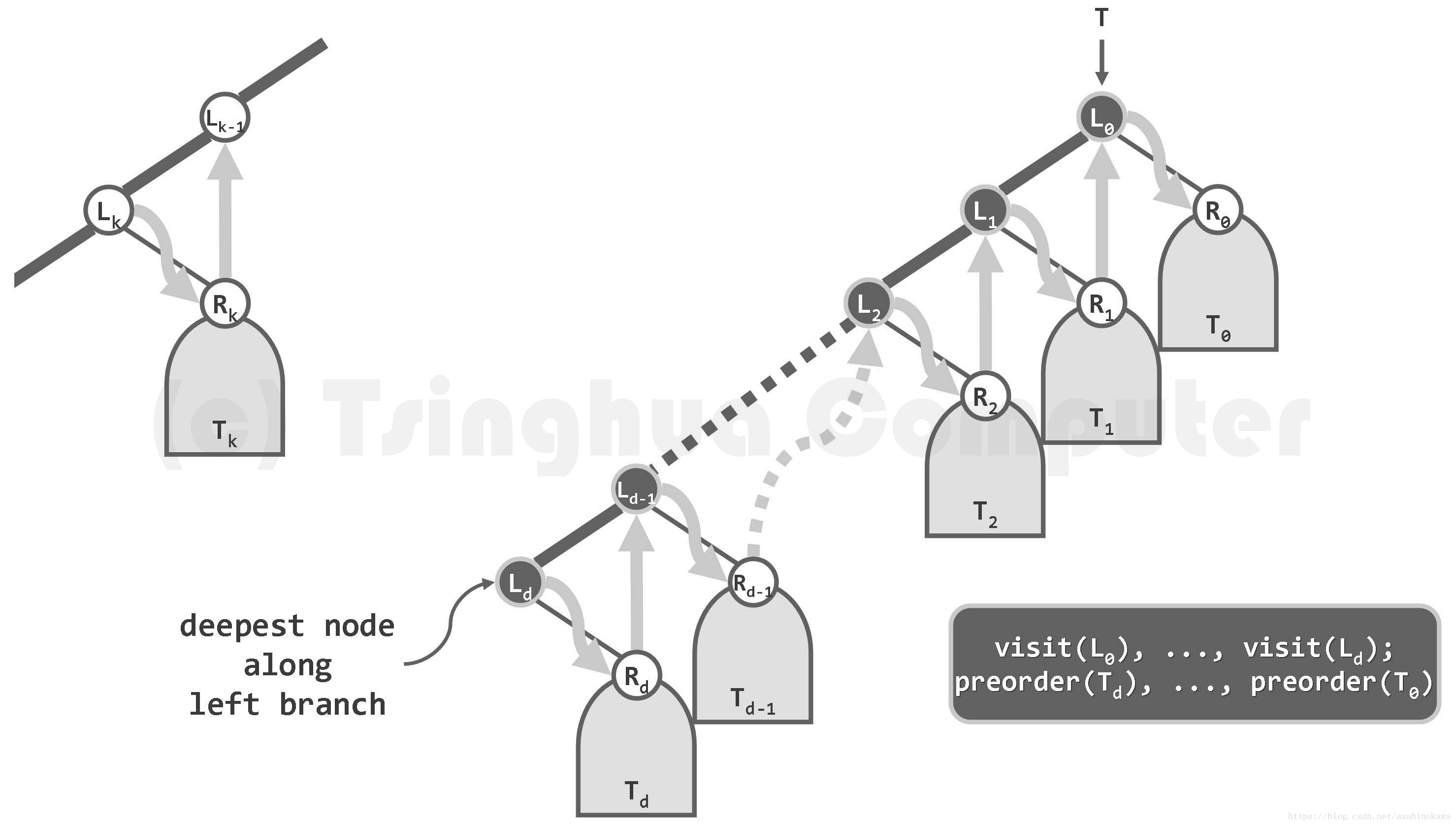
这里写图片描述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/******************************************************************************************
 * Data Structures in C++
 * ISBN: 7-302-33064-6 & 7-302-33065-3 & 7-302-29652-2 & 7-302-26883-3
 * Junhui DENG, [email protected]
 * Computer Science & Technology, Tsinghua University
 * Copyright (c) 2006-2013. All rights reserved.
 ******************************************************************************************/

#pragma once

template <typename T> //从当前节点出发，沿左分支不断深入，直至没有左分支的节点
static void goAlongLeftBranch ( BinNodePosi(T) x, Stack<BinNodePosi(T)>& S ) {
   while ( x ) { S.push ( x ); x = x->lc; } //当前节点入栈后随即向左侧分支深入，迭代直到无左孩子
}

template <typename T, typename VST> //元素类型、操作器
void travIn_I1 ( BinNodePosi(T) x, VST& visit ) { //二叉树中序遍历算法（迭代版#1）
   Stack<BinNodePosi(T)> S; //辅助栈
   while ( true ) {
      goAlongLeftBranch ( x, S ); //从当前节点出发，逐批入栈
      if ( S.empty() ) break; //直至所有节点处理完毕
      x = S.pop(); visit ( x->data ); //弹出栈顶节点并访问之
      x = x->rc; //转向右子树
   }
}
// 等价于上面的方法travIn_I1()，只是换了种表达方式
template <typename T, typename VST> //元素类型、操作器
void travIn_I2 ( BinNodePosi(T) x, VST& visit ) { //二叉树中序遍历算法（迭代版#2）
   Stack<BinNodePosi(T)> S; //辅助栈
   while ( true )
      if ( x ) {
         S.push ( x ); //根节点进栈
         x = x->lc; //深入遍历左子树
      } else if ( !S.empty() ) {
         x = S.pop(); //尚未访问的最低祖先节点退栈
         visit ( x->data ); //访问该祖先节点
         x = x->rc; //遍历祖先的右子树
      } else
         break; //遍历完成
}

图05-34.迭代式中序遍历实例（出栈节点以深色示意）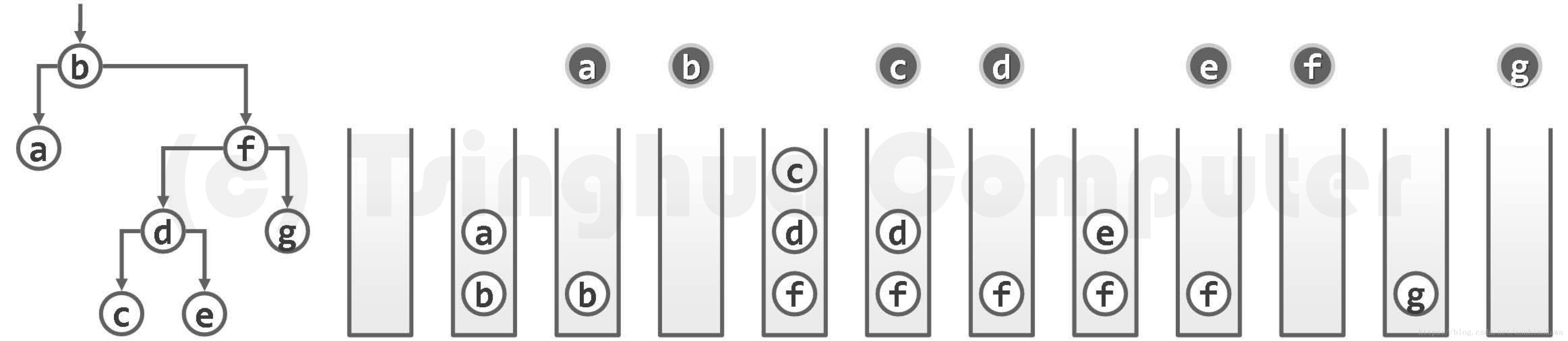
这里写图片描述

图05-35.中序遍历过程中，在无右孩子的节点处需做回溯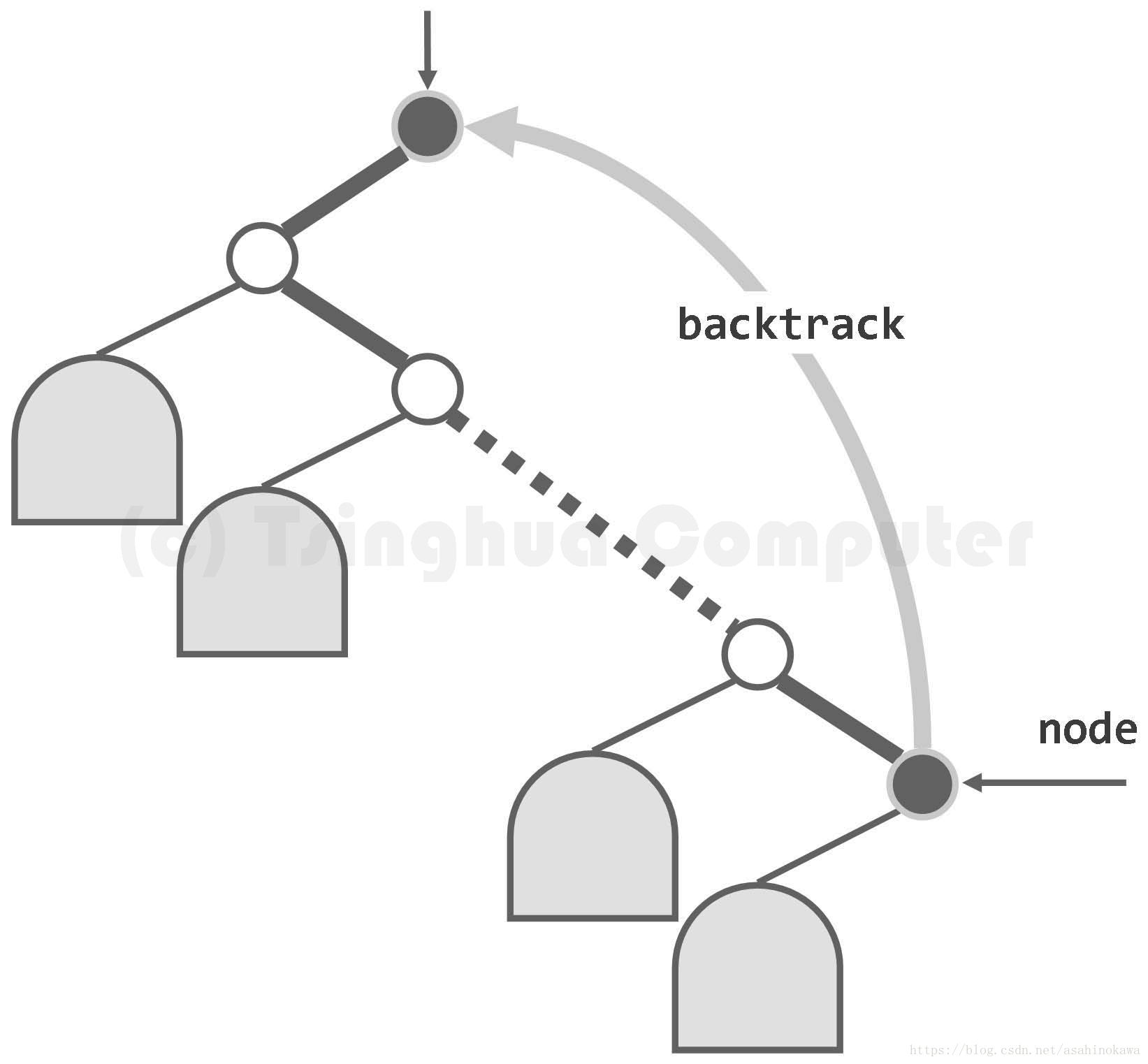
这里写图片描述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
/******************************************************************************************
 * Data Structures in C++
 * ISBN: 7-302-33064-6 & 7-302-33065-3 & 7-302-29652-2 & 7-302-26883-3
 * Junhui DENG, [email protected]
 * Computer Science & Technology, Tsinghua University
 * Copyright (c) 2006-2013. All rights reserved.
 ******************************************************************************************/
 
// 寻找此节点中序遍历的后继
template <typename T> BinNodePosi(T) BinNode<T>::succ() { //定位节点v的直接后继
   BinNodePosi(T) s = this; //记录后继的临时变量
   if ( rc ) { //若有右孩子，则直接后继必在右子树中，具体地就是
      s = rc; //右子树中
      while ( HasLChild ( *s ) ) s = s->lc; //最靠左（最小）的节点
   } else { //否则，直接后继应是“将当前节点包含于其左子树中的最低祖先”，具体地就是
      while ( IsRChild ( *s ) ) s = s->parent; //逆向地沿右向分支，不断朝左上方移动
      s = s->parent; //最后再朝右上方移动一步，即抵达直接后继（如果存在）
   }
   return s;
}

template <typename T, typename VST> //元素类型、操作器
void travIn_I3 ( BinNodePosi(T) x, VST& visit ) { //二叉树中序遍历算法（迭代版#3，无需辅助栈）
   bool backtrack = false; //前一步是否刚从右子树回溯——省去栈，仅O(1)辅助空间
   while ( true )
      if ( !backtrack && HasLChild ( *x ) ) //若有左子树且不是刚刚回溯，则
         x = x->lc; //深入遍历左子树
      else { //否则——无左子树或刚刚回溯（相当于无左子树）
         visit ( x->data ); //访问该节点
         if ( HasRChild ( *x ) ) { //若其右子树非空，则
            x = x->rc; //深入右子树继续遍历
            backtrack = false; //并关闭回溯标志
         } else { //若右子树空，则
            if ( ! ( x = x->succ() ) ) break; //回溯（含抵达末节点时的退出返回）
            backtrack = true; //并设置回溯标志
         }
      }
}

template <typename T, typename VST> //元素类型、操作器
void travIn_I4 ( BinNodePosi(T) x, VST& visit ) { //二叉树中序遍历（迭代版#4，无需栈或标志位）
   while ( true )
      if ( HasLChild ( *x ) ) //若有左子树，则
         x = x->lc; //深入遍历左子树
      else { //否则
         visit ( x->data ); //访问当前节点，并
         while ( !HasRChild ( *x ) ) //不断地在无右分支处
            if ( ! ( x = x->succ() ) ) return; //回溯至直接后继（在没有后继的末节点处，直接退出）
            else visit ( x->data ); //访问新的当前节点
         x = x->rc; //（直至有右分支处）转向非空的右子树
      }
}

后序遍历

图05-36.后序遍历过程也可划分为模式雷同的若干段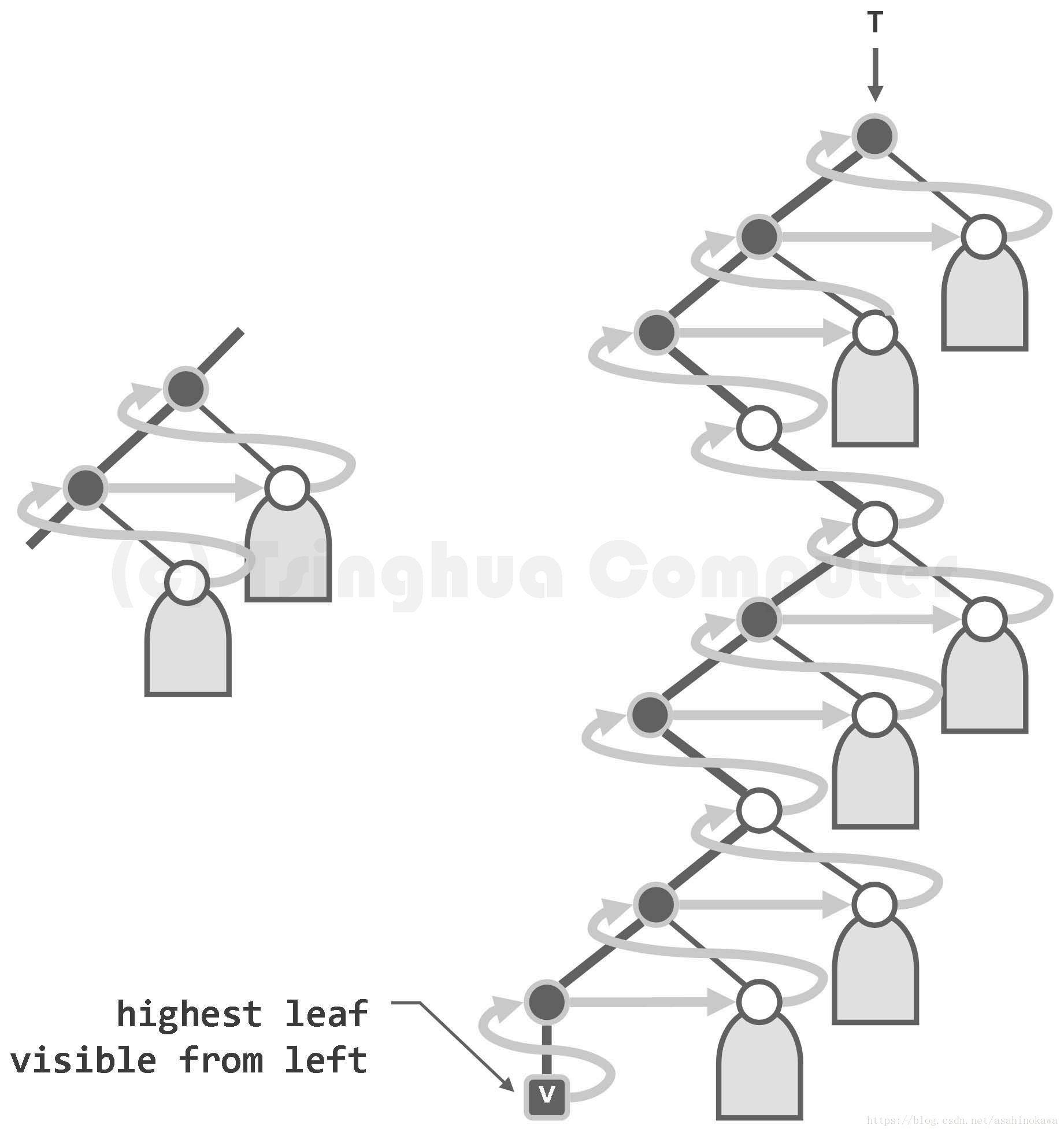
这里写图片描述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/******************************************************************************************
 * Data Structures in C++
 * ISBN: 7-302-33064-6 & 7-302-33065-3 & 7-302-29652-2 & 7-302-26883-3
 * Junhui DENG, [email protected]
 * Computer Science & Technology, Tsinghua University
 * Copyright (c) 2006-2013. All rights reserved.
 ******************************************************************************************/

#pragma once

template <typename T> //在以S栈顶节点为根的子树中，找到最高左侧可见叶节点
static void gotoHLVFL ( Stack<BinNodePosi(T)>& S ) { //沿途所遇节点依次入栈
   while ( BinNodePosi(T) x = S.top() ) //自顶而下，反复检查当前节点（即栈顶）
      if ( HasLChild ( *x ) ) { //尽可能向左
         if ( HasRChild ( *x ) ) S.push ( x->rc ); //若有右孩子，优先入栈
         S.push ( x->lc ); //然后才转至左孩子
      } else //实不得已
         S.push ( x->rc ); //才向右
   S.pop(); //返回之前，弹出栈顶的空节点
}

template <typename T, typename VST>
void travPost_I ( BinNodePosi(T) x, VST& visit ) { //二叉树的后序遍历（迭代版）
   Stack<BinNodePosi(T)> S; //辅助栈
   if ( x ) S.push ( x ); //根节点入栈
   while ( !S.empty() ) {
      if ( S.top() != x->parent ) //若栈顶非当前节点之父（则必为其右兄），此时需
         gotoHLVFL ( S ); //在以其右兄为根之子树中，找到HLVFL（相当于递归深入其中）
      x = S.pop(); visit ( x->data ); //弹出栈顶（即前一节点之后继），并访问之
   }
}

图05-37.迭代式后序遍历实例（出栈节点以深色示意，发生gotoHLVFL()调用的节点以大写字母示意）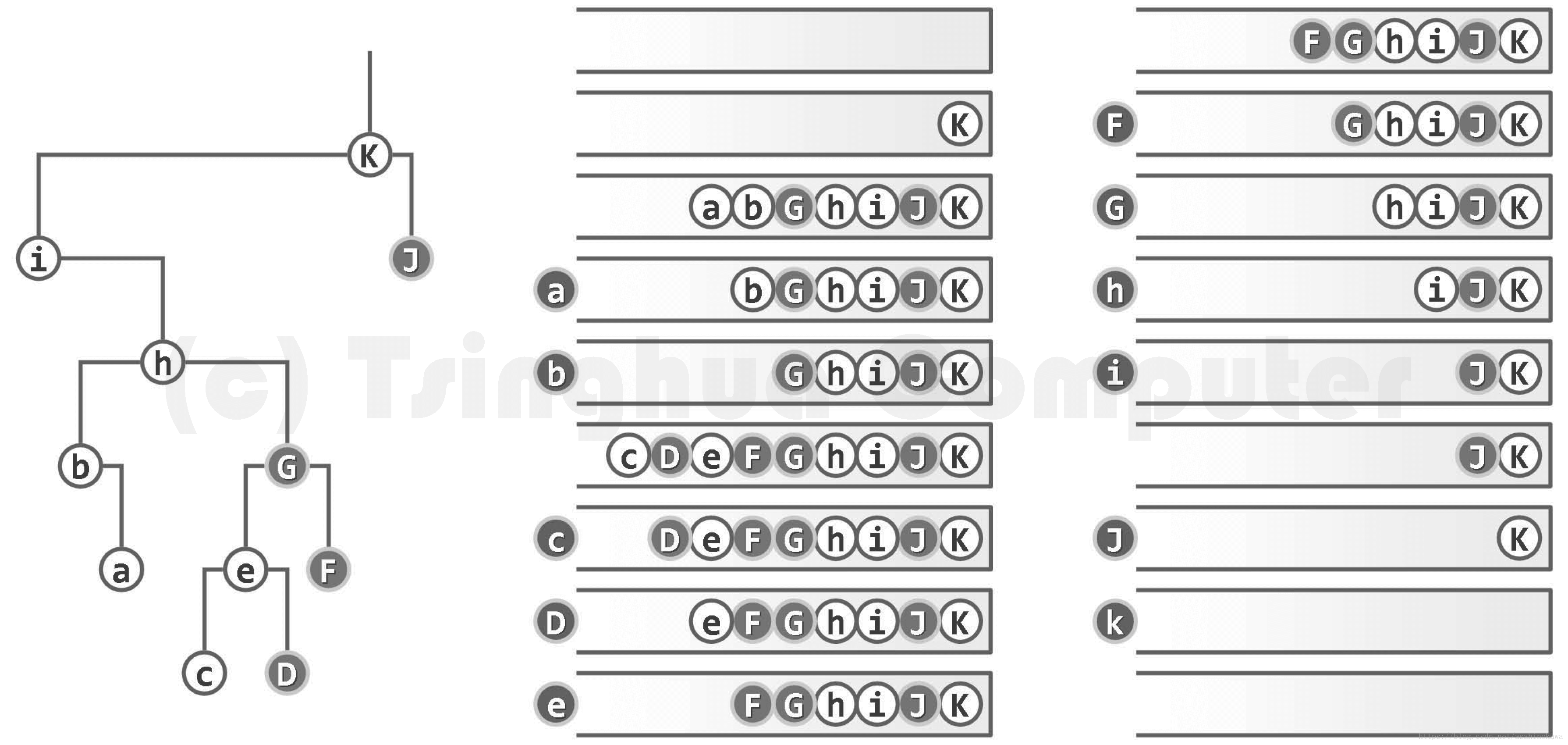
这里写图片描述

发表更新Android4 分钟读完 (大约556个字)

Android8.1原生系统网络感叹号消除

原生系统Android8.1上，WiFi上出现感叹号，此时WiFi可正常访问。原因这是Android 5.0引入的网络评估机制：就是当你连上网络后，会给目标产生204响应的服务器发送给一个请求，如果服务器返回的是状态码为204的响应，那么就被认为网络可以访问；否则，如返回的是其他状态码，那么将被视为
阅读更多

归档

最新文章

链接

×