常用排序算法

慢慢再温习一遍之前学习过的排序算法吧，一点点地积累。

插入排序

插入排序的基本思想是在遍历数组的过程中，假设在序号 i （i>=1）之前的元素即 [0..i-1] 都已经排好序，本趟需要找到 i 对应的元素 x 的正确位置 k ，并且在寻找这个位置 k 的过程中逐个将比较过的元素往后移一位，为元素 x “腾位置”，最后将 k 对应的元素值赋为 x ，一般情况下，插入排序的时间复杂度和空间复杂度分别为O(n2) 和 O(1)。（通俗说法：把数组后面那些没排序的元素换到数组前面已经排好序的部分里对应的位置）

例如：45 80 48 40 22 78
第一轮：45 80 48 40 22 78 —> 45 80 48 40 22 78 i=1
第二轮：45 80 48 40 22 78 —> 45 48 80 40 22 78 i=2
第三轮：45 48 80 40 22 78 —> 40 45 48 80 22 78 i=3
第四轮：40 45 48 80 22 78 —> 22 40 45 48 80 78 i=4
第五轮：22 40 45 48 80 78 —> 22 40 45 48 78 80 i=5
(红色代表此轮要插入的元素，红色左边是已经排好序的，右边是待排序的)

/**
* @param int[] 未排序数组
* @return int[] 排完序数组
*/
public static int[] InsertSort(int[] array){
    for(int i =1;i<array.length;i++){
        int temp = array[i];
        int j = i-1;
        while(j>=0 && temp < array[j] ){
            array[j+1] = array[j];
            j--;
        }
        array[j+1] = temp;
    }
    return array;
}

选择排序

选择排序的基本思想是遍历数组的过程中，以 i 代表当前需要排序的序号，则需要在剩余的 [i+1,…n-1] 中找出其中的最小值，然后将找到的最小值与 i 指向的值进行交换。因为每一趟确定元素的过程中都会有一个选择最大值/最小值的子流程，所以人们形象地称之为选择排序。选择排序的时间复杂度和空间复杂度分别为O(n2)和O(1)。（通俗说法：每次把剩余数组里最小的选出来放在数组的前面。所以第一次选出来的就是数组里面最小的，第二次选出来的就是数组里面第二小的，依次。。。。。）

例如：45 80 48 40 22 78
第一轮：45 80 48 40 22 78 —> 22 80 48 40 45 78 i=0
第二轮：22 80 48 40 45 78 —> 22 40 48 80 45 78 i=1
第三轮：22 40 48 80 45 78 —> 22 40 45 80 48 78 i=2
第四轮：22 40 45 80 48 78 —> 22 40 45 48 80 78 i=3
第五轮：22 40 45 48 80 78 —> 22 40 45 48 78 80 i=4
(红色代表此轮需要排序的序号的元素，红色左边是已经排好序的，右边是待排序的)

/**
* @param int[] 未排序数组
* @return int[] 排完序数组
*/
public int[] sortSelect(int[] arr){
    for (int i = 0; i < arr.length-1; i++) {
        int miniPost = i;
        for (int m = i + 1; m < arr.length; m++) {
            if (arr[m] < arr[miniPost])
         　　miniPost = m;
        }
        if (arr[i] > arr[miniPost]) {
            int temp = arr[i];
            arr[i] = arr[miniPost];
            arr[miniPost] = temp;
        }
    }
    return arr;
}

归并排序

来自：https://www.cnblogs.com/chengxiao/p/6194356.html，图非常简洁明了。

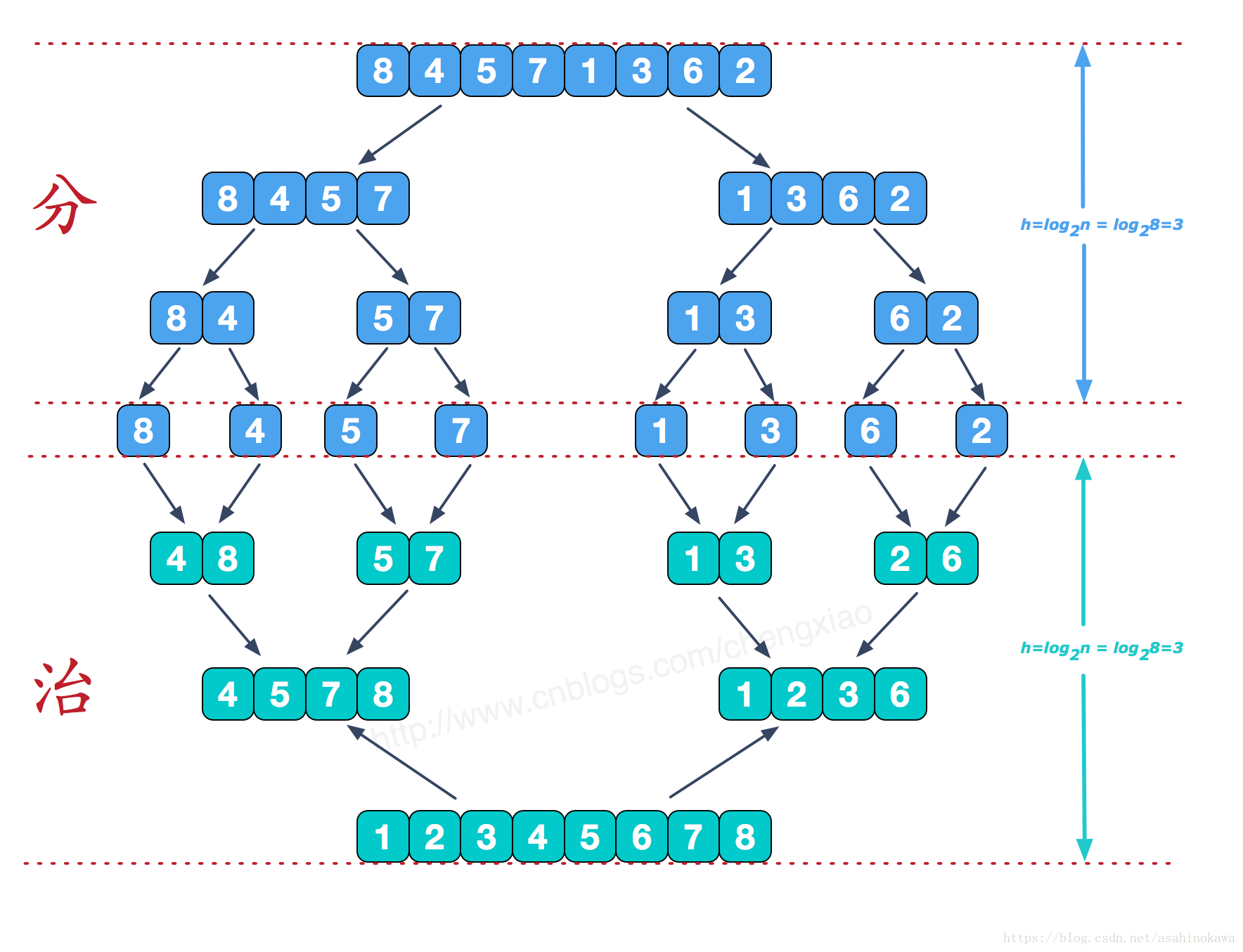
归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案”修补”在一起，即分而治之)。

分而治之

可以看到这种结构很像一棵完全二叉树，本文的归并排序我们采用递归去实现（也可采用迭代的方式去实现）。分阶段可以理解为就是递归拆分子序列的过程，递归深度为log2n。

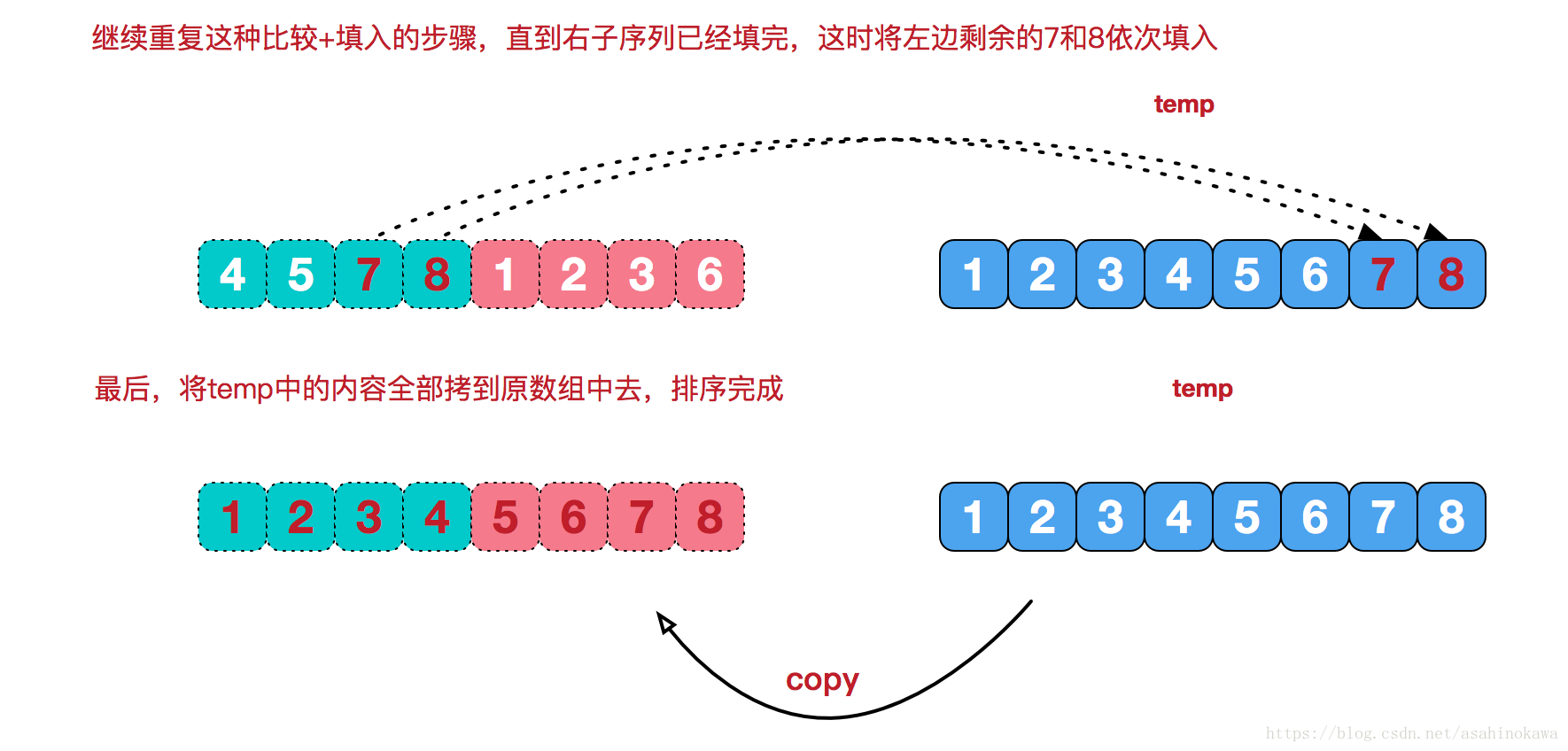
合并相邻有序子序列

再来看看治阶段，我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，来看下实现步骤。

代码实现

package sortdemo;

import java.util.Arrays;

/**
 * Created by chengxiao on 2016/12/8.
 */
public class MergeSort {
    public static void main(String []args){
        int []arr = {9,8,7,6,5,4,3,2,1};
        sort(arr);
        System.out.println(Arrays.toString(arr));
    }
    public static void sort(int []arr){
        int []temp = new int[arr.length];//在排序前，先建好一个长度等于原数组长度的临时数组，避免递归中频繁开辟空间
        sort(arr,0,arr.length-1,temp);
    }
    private static void sort(int[] arr,int left,int right,int []temp){
        if(left<right){
            int mid = (left+right)/2;
            sort(arr,left,mid,temp);//左边归并排序，使得左子序列有序
            sort(arr,mid+1,right,temp);//右边归并排序，使得右子序列有序
            merge(arr,left,mid,right,temp);//将两个有序子数组合并操作
        }
    }
    private static void merge(int[] arr,int left,int mid,int right,int[] temp){
        int i = left;//左序列指针
        int j = mid+1;//右序列指针
        int t = 0;//临时数组指针
        while (i<=mid && j<=right){
            if(arr[i]<=arr[j]){
                temp[t++] = arr[i++];
            }else {
                temp[t++] = arr[j++];
            }
        }
        while(i<=mid){//将左边剩余元素填充进temp中
            temp[t++] = arr[i++];
        }
        while(j<=right){//将右序列剩余元素填充进temp中
            temp[t++] = arr[j++];
        }
        t = 0;
        //将temp中的元素全部拷贝到原数组中
        while(left <= right){
            arr[left++] = temp[t++];
        }
    }
}

/**
执行结果
[1, 2, 3, 4, 5, 6, 7, 8, 9]
**/

归并排序是稳定排序，它也是一种十分高效的排序，能利用完全二叉树特性的排序一般性能都不会太差。java中Arrays.sort()采用了一种名为TimSort的排序算法，就是归并排序的优化版本。从上文的图中可看出，每次合并操作的平均时间复杂度为O(n)，而完全二叉树的深度为|log2n|。总的平均时间复杂度为O(nlogn)。而且，归并排序的最好，最坏，平均时间复杂度均为O(nlogn)。

快速排序

大概的思想是（假设为升序），先以一个数为参照，然后将所有的大于它的数移到它的后面，小于它的数移到前面，再以此数的位置，将数组分成两部分，再对这两部分做相同的操作…如此递归，直至完毕。

public static void main(String[] args) {
    int[] arr = new int[]{6,2,4,99,22,56,11,5,7,4,1};
    QuickSort(arr, 0, arr.length - 1);
    printArray(arr);
}

static void QuickSort(int[] arr, int left, int right){
    if (left > right)
        return;
    int pivot_index = partition1(arr, left, right);
    QuickSort(arr, left, pivot_index - 1);
    QuickSort(arr, pivot_index + 1, right);
}

static int partition1(int[] arr, int left, int right){
    int pivot = arr[left];
    while(left < right){
        while(left < right && arr[right] >= pivot){
            right--;
        }
        arr[left] = arr[right];

        while(left < right && arr[left] <= pivot){
            left++;
        }
        arr[right] = arr[left];

    }
    arr[left] = pivot;
    return left;
}