大意
如果有一个 random9() 函数,可以产生 1-9 的 整数随机数,请利用 random9 实现 random10 函数,返回 1-10 的整数随机数
要点
random9 只能随机产生 1-9 范围内的数,也就是 1-9 出现的概率是一样的;而如果要随机产生 1-10 范围的整数,就需要 1-10 出现的概率是一样的。
所以问题就变成了:如何通过等概率出现的 1-9 产生等概率的 1-10 ?
解决
以一种马后炮的思想尝试解释一下,看能不能说服自己。
random9 显然产生不了 10,所以肯定需要用到加/乘法,那如何产生 10?
random9 + n
如果只用加法,这样便可以随机产生[n+1, n+9]范围的整数,可以达到10,但是肯定不能产生[1, 10]范围内的数,所以这样不行。random9 * n
如果只用乘法,这样便可以随机产生[n, 2n, 3n, …, 9n],这样产生的数显然也不可能做到随机产生[1, 10],因为中间存在空位,并且无法保证是等概率的。
要想等概率产生[1, 10]范围的数,可以利用等概率产生[1, 20]范围的整数,然后%10 + 1。这里有个重点,怎么样才能等概率?
既然 random9 加/乘一个固定的数,不能达到目的,那么如果加/乘一个不固定但是等概率出现的某一范围的数(也就是 random9)是否可行呢?
random9 + random9
能出现的最大数:9 + 9 = 18;能出现的最小数:1 + 1 = 2
先考虑能否等概率出现10,先看2-18是否为等概率出现的。
出现2、18的概率都是1/81,但出现3的概率是2/81,即1+2和2+1,这个就不是等概率出现的了,所以不能做到随机产生。random9 * random9
最大数:81,最小数:1。
是否连续?否。
是否等概率?否。最大、小数的概率是1/81。但是9的概率是3/81。random9 * n + random9
random9 * n 可等概率产生 1n,2n,3n…9n,如果加上 random9,是否等概率取决于1n和2n之间的间距,如果刚好等于9,那么加上random9就有希望产生连续、并且等概率的整数,范围为:[10, 90]。
如何通过等随机产生的 [10, 90] 来随机产生 [1, 10]?
将随机产生的 [10, 90] 限制为 [10, 89],然后模10,便可以获得随机产生的[0, 9],然后再加1,即可得到随机产生的[1, 10]。
总结为:先通过 random9 * 9 + random9 随机产生[10, 90]范围的整数,然后限制随机产生 [10, 89],再模10,得到[0, 9],再加1即可得到[1, 10]。
所以最终的代码:
1 | while ((result = 9 * random9() + random9()) >= 90); |
但是,我看到的答案是这样的,还不太明白这两者之间有什么差别。
1 | public int rand10() { |
更加简单粗暴的方式
但是这个问题是由 random7 求 random10,不过思想是相通的。
感觉这一种方式更加通俗易懂,获取一维数组是随机的,获取第二维数组也是随机,整个过程都是随机的。
1 | public static int random10() { |
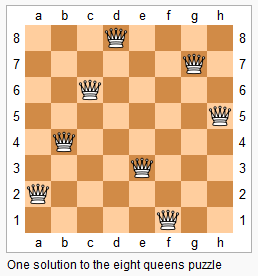
N皇后问题
1 | import java.util.ArrayList; |
Letter Combinations of a Phone Number
Given a string containing digits from 2-9 inclusive, return all possible letter combinations that the number could represent.
A mapping of digit to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.

1 | import java.util.ArrayList; |
Generate Parentheses
Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.
For example, given n = 3, a solution set is:
1 | [ |
1 | class Solution { |
Sudoku Solver
Write a program to solve a Sudoku puzzle by filling the empty cells.
A sudoku solution must satisfy all of the following rules:
Each of the digits 1-9 must occur exactly once in each row.
Each of the digits 1-9 must occur exactly once in each column.
Each of the the digits 1-9 must occur exactly once in each of the 9 3x3 sub-boxes of the grid.
Empty cells are indicated by the character ‘.’.
1 | /* |
Combination Sum

相关问题:Combination Sum II
1 |
|
Permutations
相关问题:Permutations II
1 | class Solution { |
Permutation Sequence

1 | class Solution { |
Combinations
1 | class Solution { |
【leetcode】21. Merge Two Sorted Lists
Merge two sorted linked lists and return it as a new list. The new list should be made by splicing together the nodes of the first two lists.
Example:
Input: 1->2->4, 1->3->4
Output: 1->1->2->3->4->4
题目属于简单类型,但是好久没写这种题了,再加上C语言也很久没写过了,费了很久。。。
思路很简单,先以一个为基准,然后再将另外一个逐个插入其中(然而开始的时候并不是这么想的,用的某种骚操作,结果发现写着写着搞不定了,这种写代码的方式果然不行呀)。感觉还可以有提高的地方,比如用个二分什么的。
1 | /** |
https://leetcode.com/problems/integer-to-roman/
1 | char ONE[5] = {' ', 'I', 'X', 'C', 'M'}; |
https://leetcode.com/problems/roman-to-integer/
1 | int getRomanValue(char ch) { |
终于到写这篇的时候了。这是一篇对于邓俊辉的《数据结构(C++语言版)(第3版)》中二叉树遍历部分的读书笔记,图片来自DSACPP。感觉这本书很用心。当初要买这本书的原因也就是看到了他对迭代式遍历二叉树的这些内容,很赞。
先序遍历
图05-32.先序遍历过程:先沿左侧通路自顶而下访问沿途节点,再自底而上依次遍历这些节点的右子树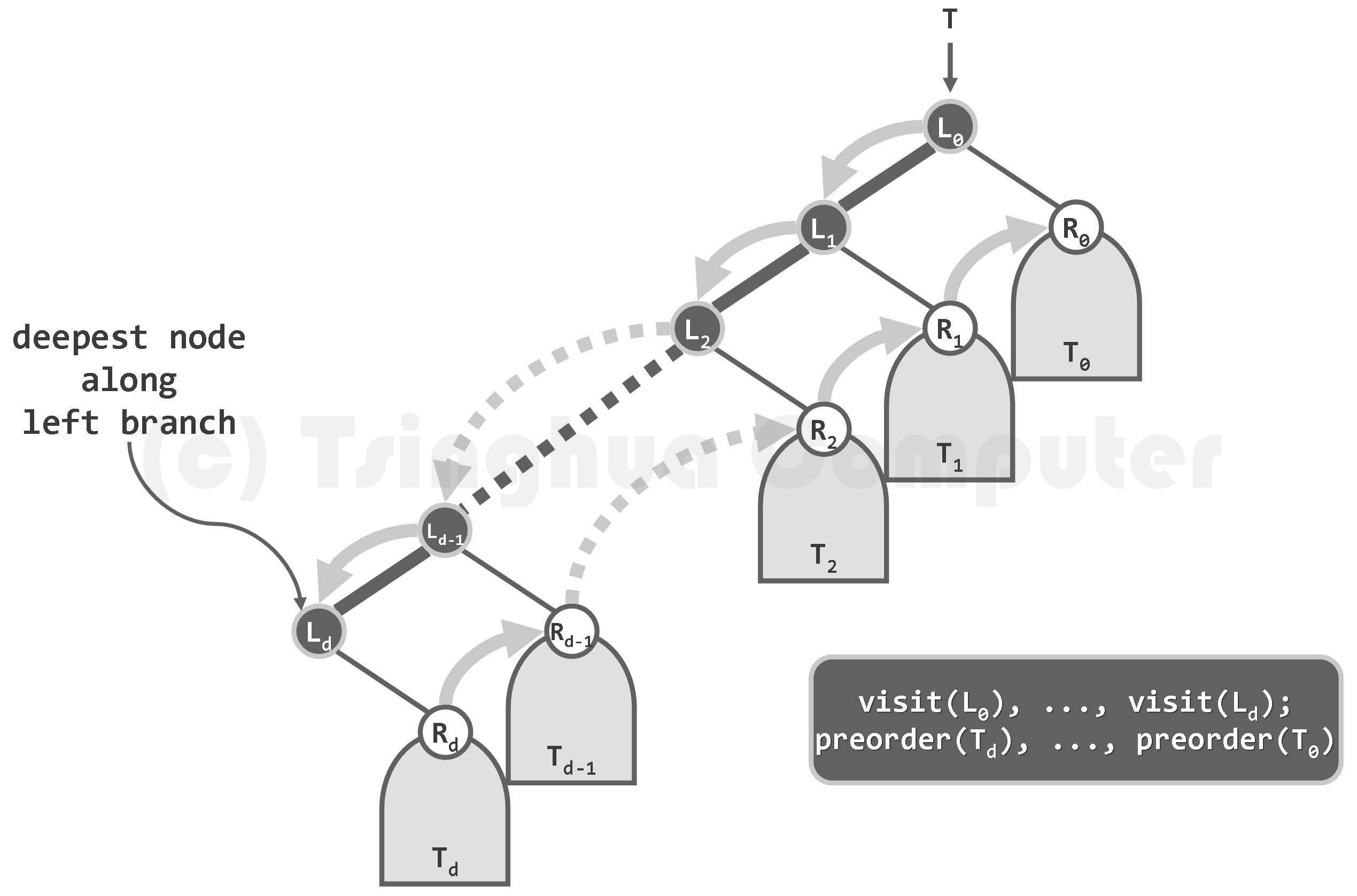
1 | /****************************************************************************************** |
图05-31.迭代式先序遍历实例(出栈节点以深色示意)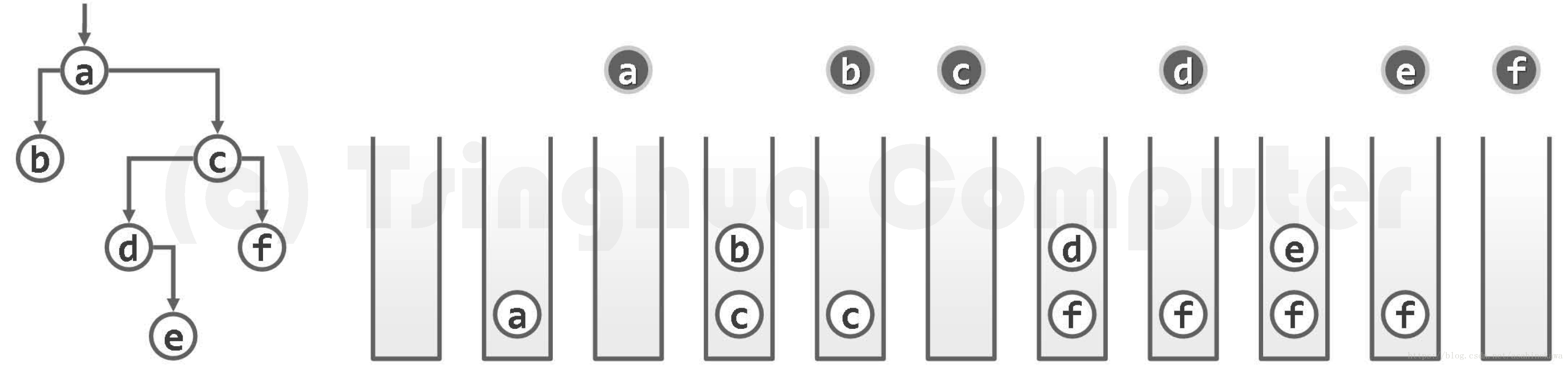
中序遍历
图05-33.中序遍历过程:顺着左侧通路,自底而上依次访问沿途各节点及其右子树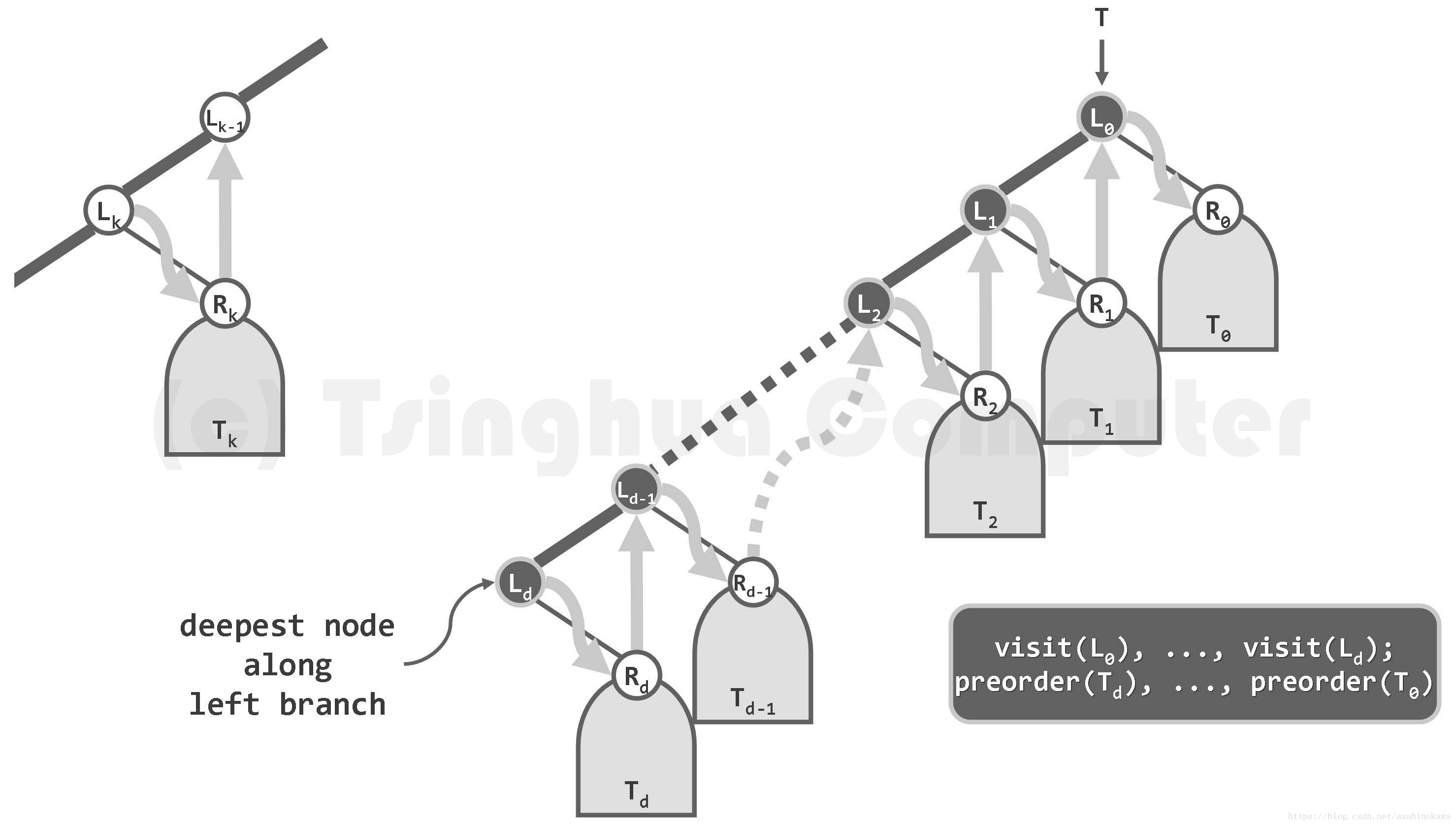
1 | /****************************************************************************************** |
图05-34.迭代式中序遍历实例(出栈节点以深色示意)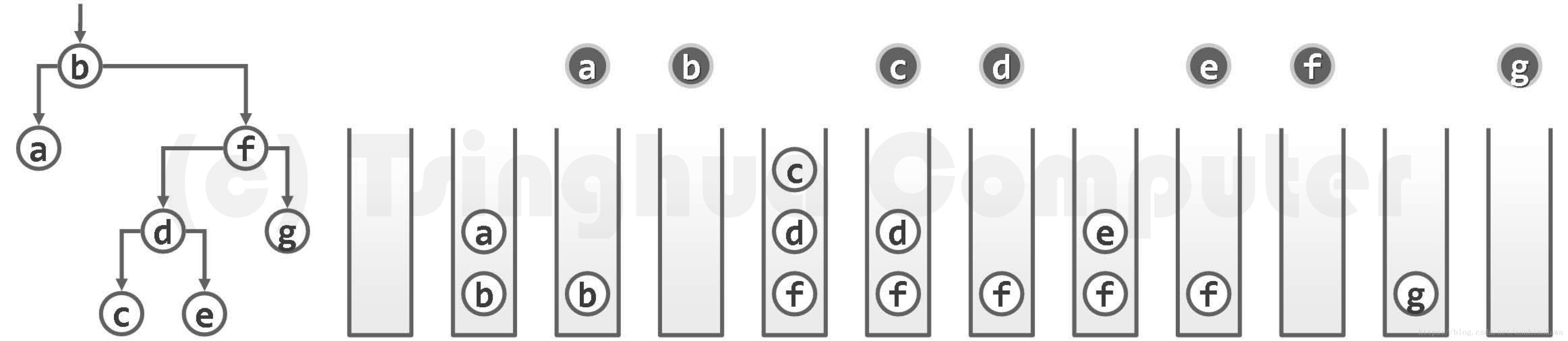
图05-35.中序遍历过程中,在无右孩子的节点处需做回溯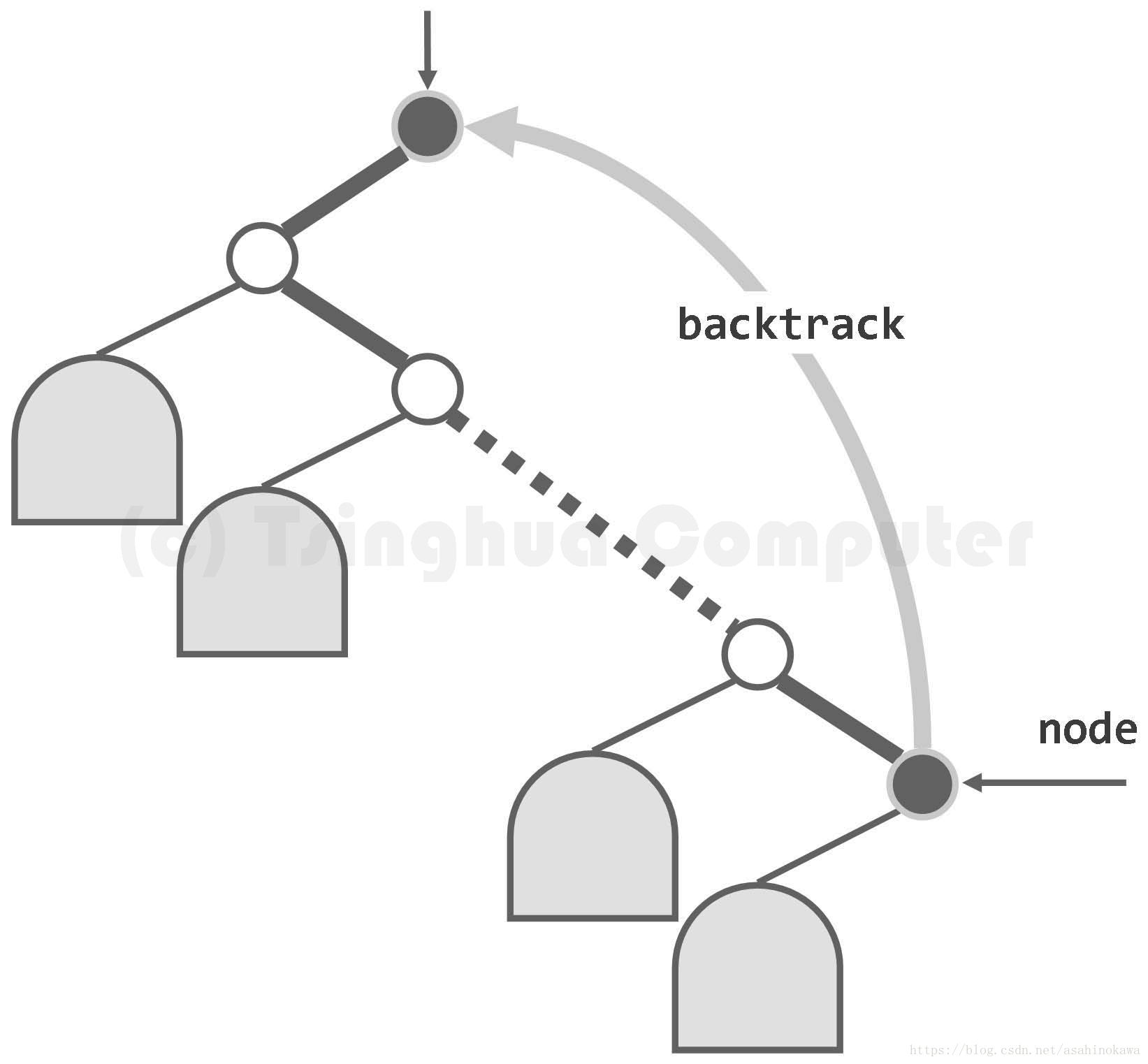
1 | /****************************************************************************************** |
后序遍历
图05-36.后序遍历过程也可划分为模式雷同的若干段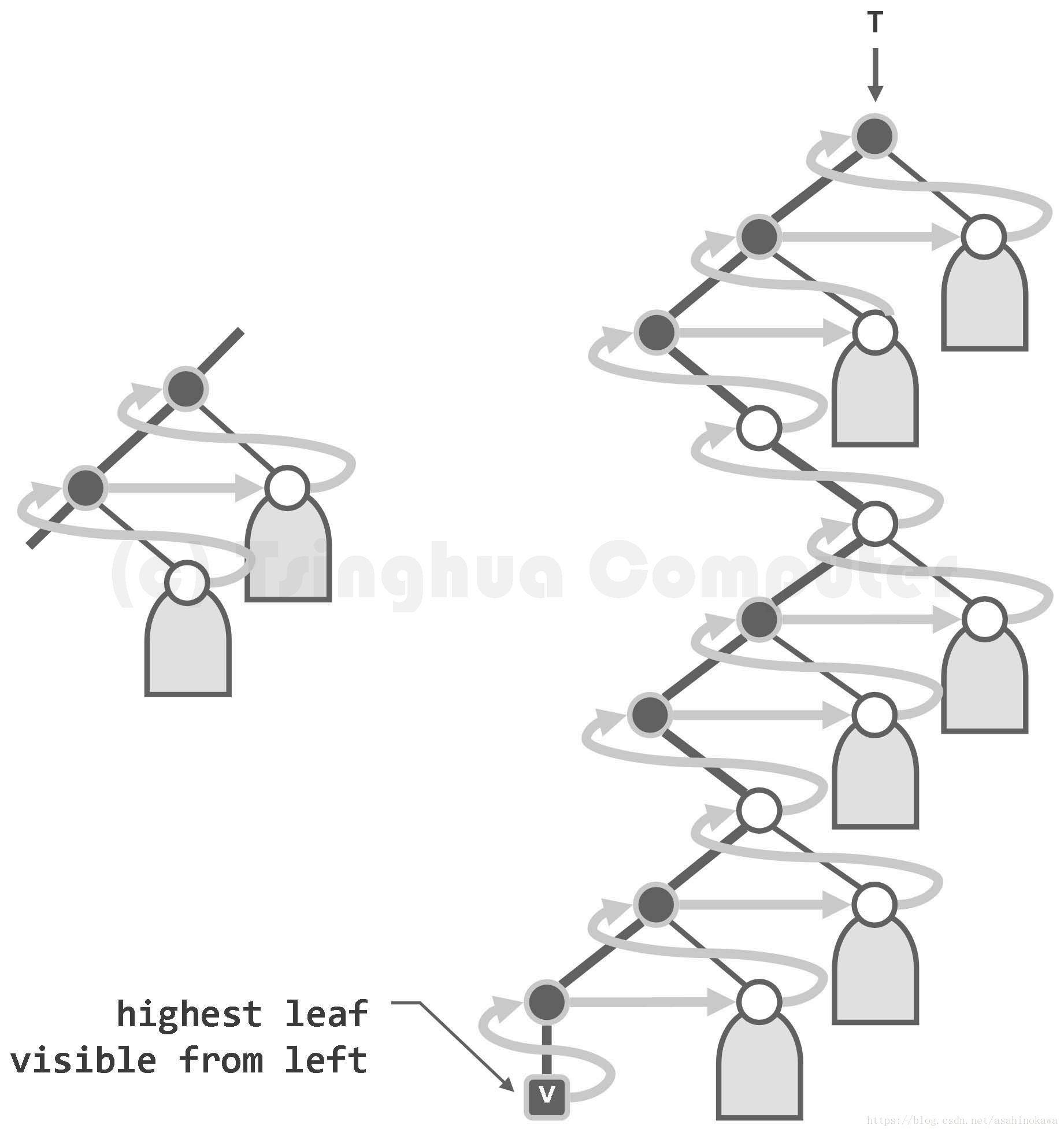
1 | /****************************************************************************************** |
图05-37.迭代式后序遍历实例(出栈节点以深色示意,发生gotoHLVFL()调用的节点以大写字母示意)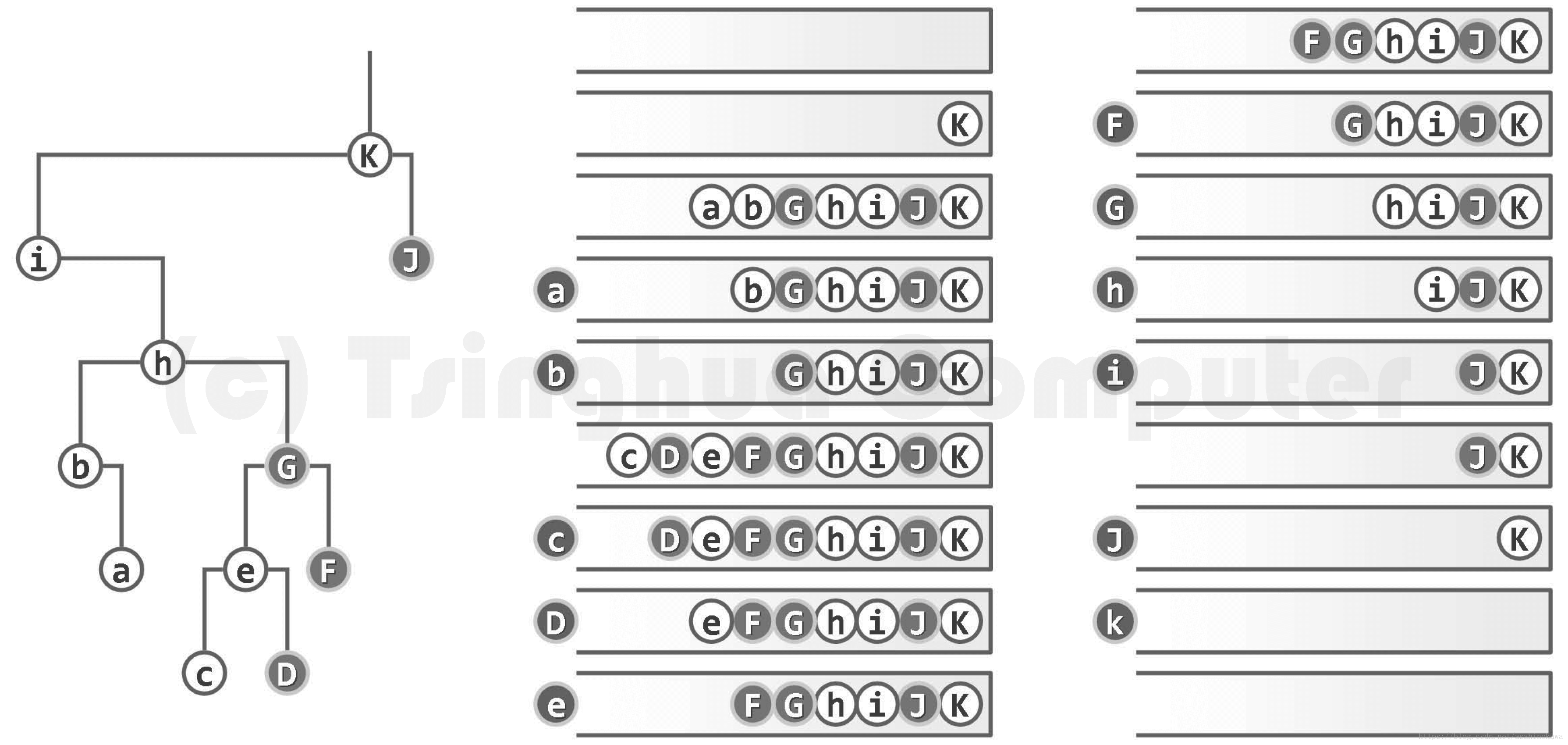
慢慢再温习一遍之前学习过的排序算法吧,一点点地积累。
插入排序
插入排序的基本思想是在遍历数组的过程中,假设在序号 i (i>=1)之前的元素即 [0..i-1] 都已经排好序,本趟需要找到 i 对应的元素 x 的正确位置 k ,并且在寻找这个位置 k 的过程中逐个将比较过的元素往后移一位,为元素 x “腾位置”,最后将 k 对应的元素值赋为 x ,一般情况下,插入排序的时间复杂度和空间复杂度分别为O(n2) 和 O(1)。(通俗说法:把数组后面那些没排序的元素换到数组前面已经排好序的部分里对应的位置)
例如:45 80 48 40 22 78
第一轮:45 80 48 40 22 78 —> 45 80 48 40 22 78 i=1
第二轮:45 80 48 40 22 78 —> 45 48 80 40 22 78 i=2
第三轮:45 48 80 40 22 78 —> 40 45 48 80 22 78 i=3
第四轮:40 45 48 80 22 78 —> 22 40 45 48 80 78 i=4
第五轮:22 40 45 48 80 78 —> 22 40 45 48 78 80 i=5
(红色代表此轮要插入的元素,红色左边是已经排好序的,右边是待排序的)
1 | /** |
选择排序
选择排序的基本思想是遍历数组的过程中,以 i 代表当前需要排序的序号,则需要在剩余的 [i+1,…n-1] 中找出其中的最小值,然后将找到的最小值与 i 指向的值进行交换。因为每一趟确定元素的过程中都会有一个选择最大值/最小值的子流程,所以人们形象地称之为选择排序。选择排序的时间复杂度和空间复杂度分别为O(n2)和O(1)。(通俗说法:每次把剩余数组里最小的选出来放在数组的前面。所以第一次选出来的就是数组里面最小的,第二次选出来的就是数组里面第二小的,依次。。。。。)
例如:45 80 48 40 22 78
第一轮:45 80 48 40 22 78 —> 22 80 48 40 45 78 i=0
第二轮:22 80 48 40 45 78 —> 22 40 48 80 45 78 i=1
第三轮:22 40 48 80 45 78 —> 22 40 45 80 48 78 i=2
第四轮:22 40 45 80 48 78 —> 22 40 45 48 80 78 i=3
第五轮:22 40 45 48 80 78 —> 22 40 45 48 78 80 i=4
(红色代表此轮需要排序的序号的元素,红色左边是已经排好序的,右边是待排序的)
1 | /** |
归并排序
来自:https://www.cnblogs.com/chengxiao/p/6194356.html,图非常简洁明了。
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案”修补”在一起,即分而治之)。
分而治之
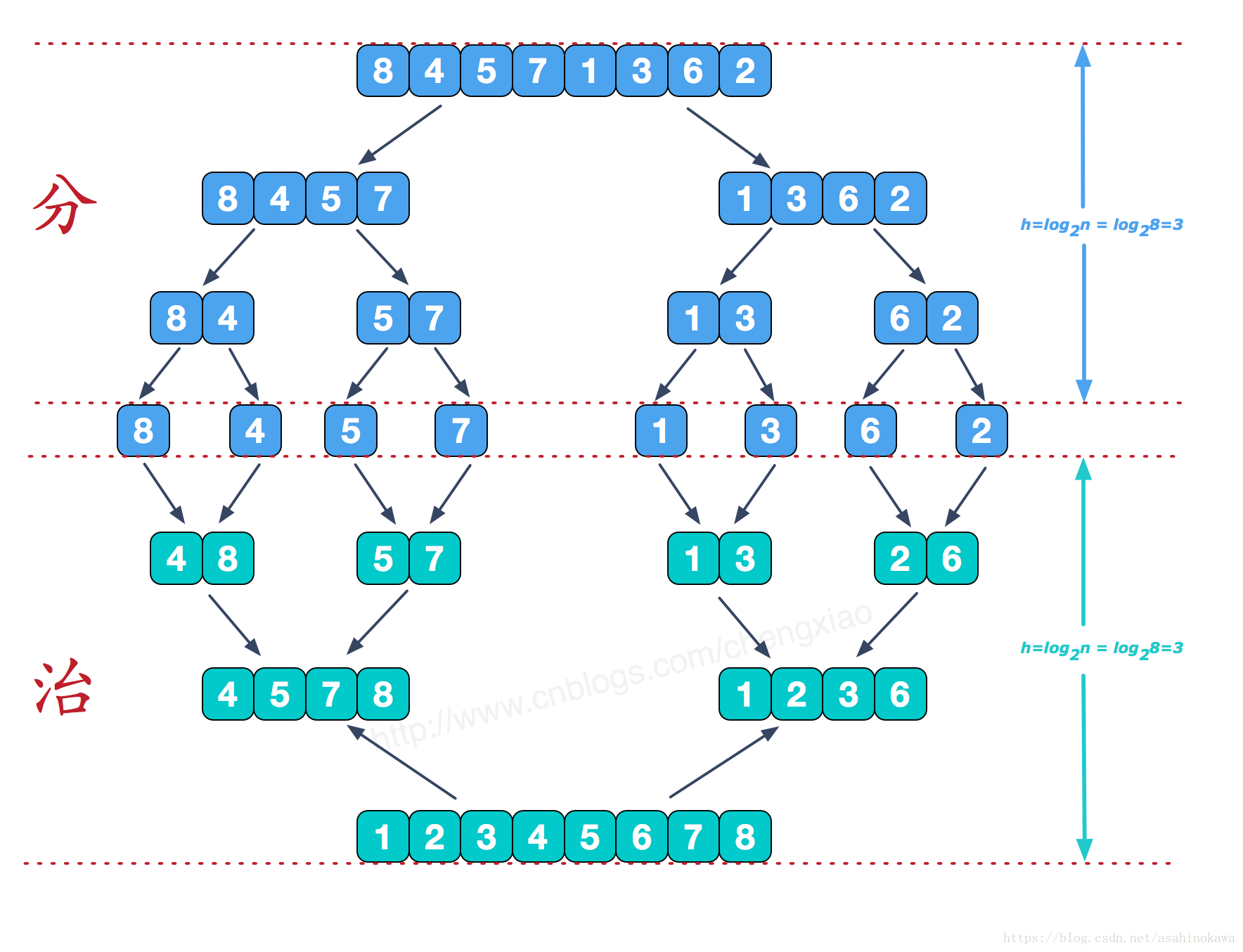
可以看到这种结构很像一棵完全二叉树,本文的归并排序我们采用递归去实现(也可采用迭代的方式去实现)。分阶段可以理解为就是递归拆分子序列的过程,递归深度为log2n。
合并相邻有序子序列
再来看看治阶段,我们需要将两个已经有序的子序列合并成一个有序序列,比如上图中的最后一次合并,要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列,合并为最终序列[1,2,3,4,5,6,7,8],来看下实现步骤。
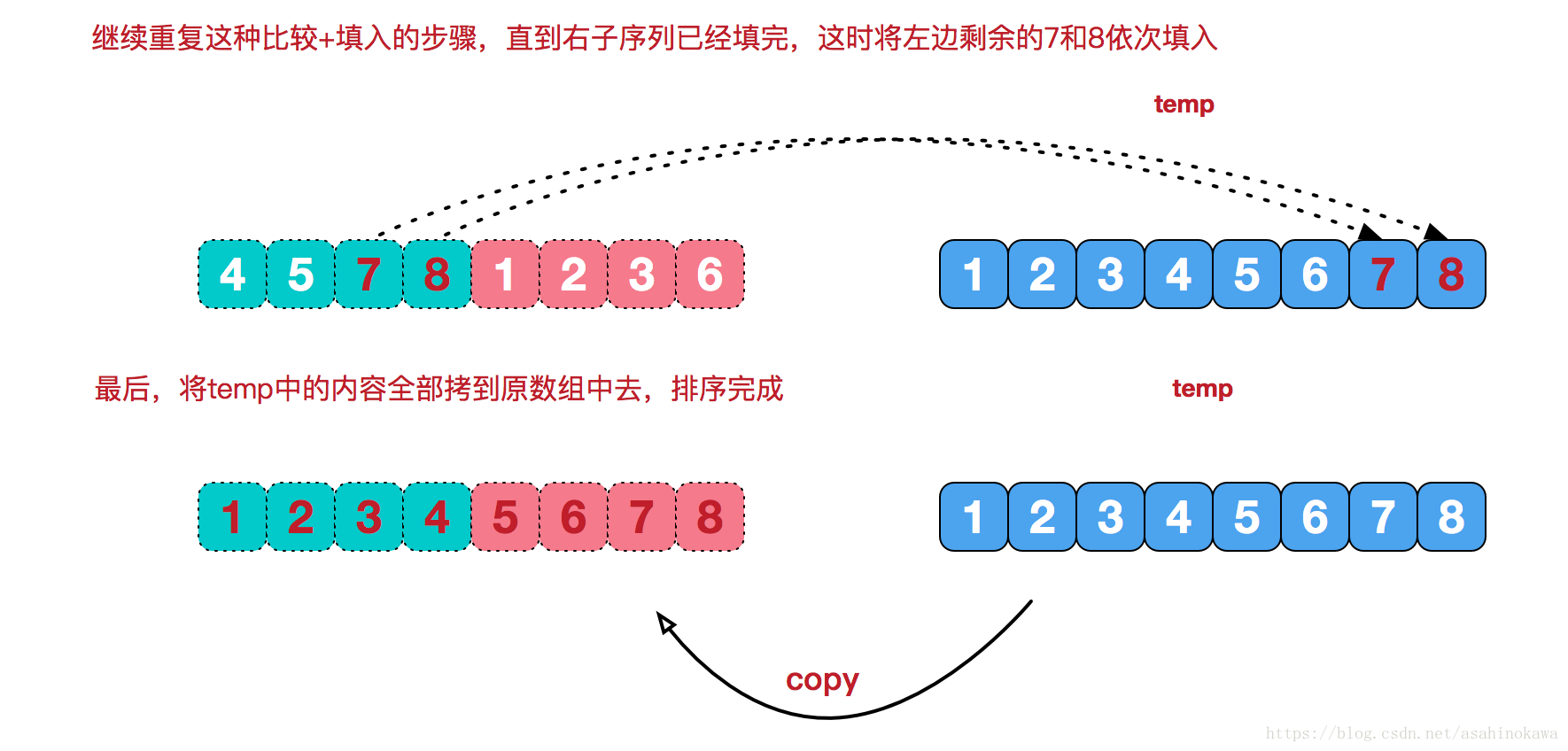
代码实现
1 | package sortdemo; |
归并排序是稳定排序,它也是一种十分高效的排序,能利用完全二叉树特性的排序一般性能都不会太差。java中Arrays.sort()采用了一种名为TimSort的排序算法,就是归并排序的优化版本。从上文的图中可看出,每次合并操作的平均时间复杂度为O(n),而完全二叉树的深度为|log2n|。总的平均时间复杂度为O(nlogn)。而且,归并排序的最好,最坏,平均时间复杂度均为O(nlogn)。
快速排序
大概的思想是(假设为升序),先以一个数为参照,然后将所有的大于它的数移到它的后面,小于它的数移到前面,再以此数的位置,将数组分成两部分,再对这两部分做相同的操作…如此递归,直至完毕。
1 | public static void main(String[] args) { |




